Rife-Vincent Windowing Function
Introduction
Windowing Functions are used in signal processing like spectral analysis to crop a signal to the range of interest. The main differences between the Windowing functions are their properties in the frequency domain: main-lobe bandwidth (pass-band) and height of side-lobes in the stop-band. Optimizing pass-band and stop-band properties is a concurrent problem: lowering the side-lobes usually comes with a broader main-lobe. For more detailed information see http://en.wikipedia.org/wiki/Windowing_functions.
Popular Windowing Functions
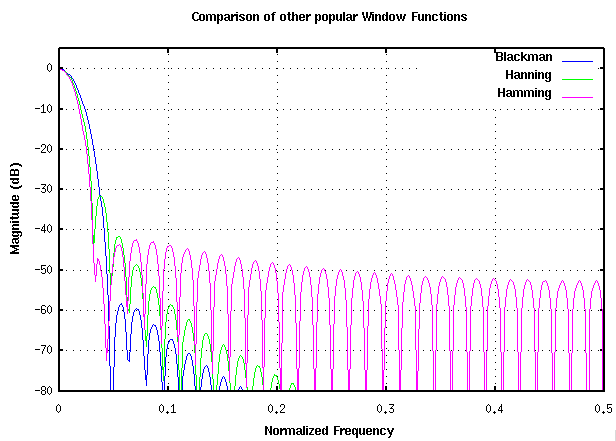
Most literature and the Internet (e.g. Wikipedia) mention a range of filters, making them quite popular and common knowledge: the Hamming, Hanning, Blackman and Blackman-Harris window. These windows are readily available in numerical computation software like Matlab and GNU Octave and are also often used to introduce students to the subject at University.
The Rife-Vincent window
The Rife-Vincent windowing function though does not get much attention in the public domain, even though it outperforms any of the windows mentioned before. Octave´s signal package and Matlab don´t come with a function for generating a Rife-Vincent window, and Wikipedia only mentions it without formerly defining its equation or any of its properties.

The general Rife-Vincent window is defined as
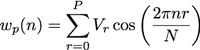
where it´s coefficients Vr are defined as
| P | r = 0 | r = 1 | r = 2 | r = 3 | r = 4 |
|---|---|---|---|---|---|
| 1 | 1/2 | -1/2 | N/A | N/A | N/A |
| 2 | 3/8 | -4/8 | 1/8 | N/A | N/A |
| 3 | 10/32 | -15/32 | 6/32 | -1/32 | N/A |
| 4 | 35/128 | -56/128 | 28/128 | -8/128 | 1/128 |
With grade 4 the equation transforms to
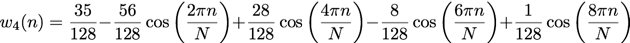
Conclusion
Even though not widely adopted, the Rife-Vincent window outperforms all popular windowing functions. Calculating the window samples is as computationally efficient as for any of the other popular functions. The high decay in the stop-band makes the Rife-Vincent4 window the window-of-choice.
Links
Octave source code used to plot the functions: WindowingFunctions.m
Vladimir Haasz: "System for Quality Testing of Ripple Control Receiver", Faculty of Electrical Engineering, Czech Technical University in Prag:
http://measure.feld.cvut.cz/usr/staff/haasz/publications/p32.pdf